Optimal design of container in extended container movable house (end)
2. Container optimization designFrom the viewpoint of saving cost and reducing the weight of the box, the box part is optimized. A set of design data should be sought to make the maximum stress of the structure under the most unfavorable working condition of top lifting less than 200MPa, the maximum deflection of the long beam on the bottom less than 6mm, and minimize the self weight of the box. This optimization analysis is carried out for the improved container. According to the previous calculation and analysis, it can be seen that the design of four columns and four beams of the container is mature, so it will not be considered in the optimization analysis. Since the main components such as beams and columns have been analyzed and calculated with plate and shell element, in order to reduce the iteration time of optimal design, beam element is selected for other components except for the plate and shell element simulation of corrugated plate. In this analysis, the section dimensions (width, height and thickness) of top long beam, bottom long beam, bottom short beam and bottom auxiliary long beam are taken as optimization parameters, with a total of 16 optimization variables. The constraint condition is: the maximum stress Rmax of all elements is less than 200MPa; The maximum deflection Dmax of the long beam at the bottom is less than 6mm, and the maximum deflection Dmax of the short beam at the bottom is less than 13mm. The optimization objective is to minimize the total mass of the box. The name and value range of optimization variables are shown in Table 2.
Table 2 name and value range of optimization design variables
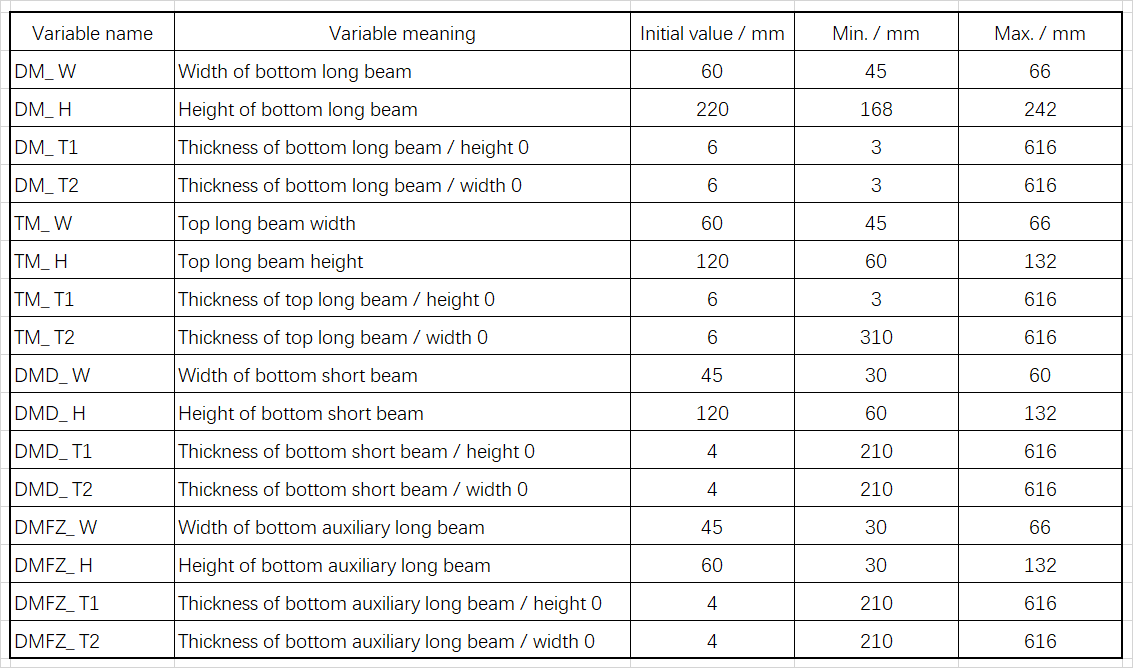
Table 3 final values of design variables
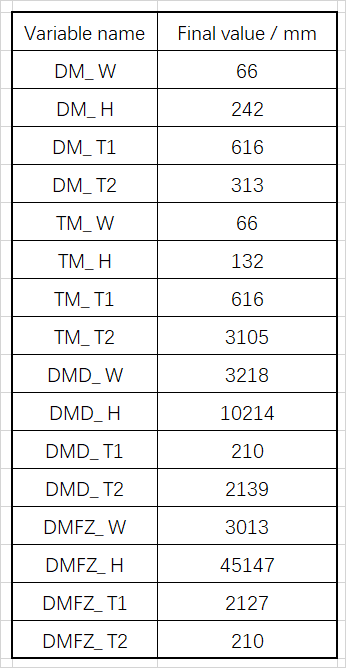
Fig. 6 optimization process of objective function
The following is the calculation results of container optimization design during uniform lifting (the results of other working conditions will not be listed). The load and boundary conditions are the same as those before optimization design. The calculation results are shown in Figure 8 and Figure 9.
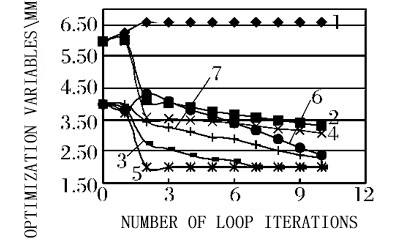
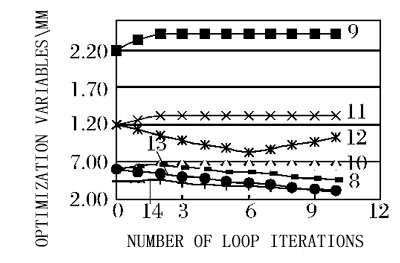
1 - thickness value of bottom long beam / height 0; 2 - thickness value of bottom long beam / width 0;
3 - thickness value of top long beam / height 0; 4 - thickness value of top long beam / width 0;
5 - thickness value of bottom short beam / height 0; 6 - thickness value of bottom short beam / height 0;
7 - bottom auxiliary long beam / width 0; 8 - width value of long beam at the bottom;
9 - height value of long beam at the bottom; 10 - height value of top long beam;
11 - height value of top long beam; 12 - height value of bottom short beam;
13 - width value of bottom short beam; 14 - width value of bottom auxiliary long beam
Fig. 7 optimization process of design variables
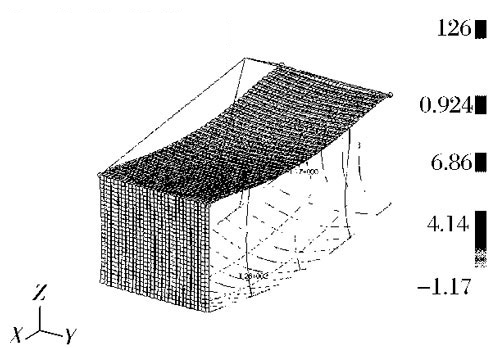
Fig. 8 stress field distribution of box after optimized design
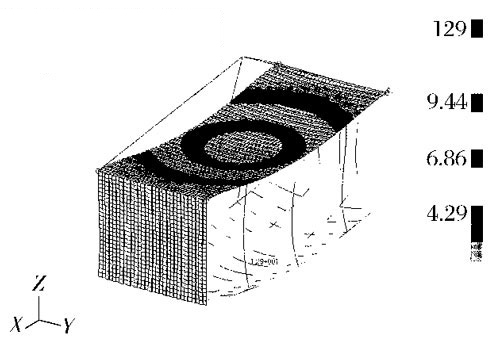
Figure 9 displacement field distribution of box body after optimized design
3. Conclusion
The stress of the improved container under various loading and unloading conditions is simulated and calculated. At the same time, the section size of the box under the most unfavorable working condition of uniform lifting is optimized with the idea of optimization design, so as to reduce the self weight of the box. After calculation, the weight of the box body is reduced by 15% after the optimization design. Compared with that before the optimization design, the maximum stress of the box is reduced from 162mpa to 126mpa, and the position of the maximum stress also changes; However, the maximum deformation increases from 8181mm to 1219mm, which is located in the center of the bottom short beam and auxiliary long beam; The stress and deflection of the main stressed member - the long beam at the bottom are reduced.
Relevant contents: